G. W. Leibniz
[sc name=”grevenue” ][/sc]Em Deus, existência é o mesmo que essência; ou – colocando diferentemente a mesma coisa – existir é essencial para Deus. Então, Deus é um ser necessário, um ser que existe necessariamente.
As coisas criadas são contingentes, isto é, suas existências não se inferem se suas essências.
Verdades necessárias são aquelas que podem ser demonstradas através de uma análise de termos, de modo que resultam em identidades. Por exemplo, um quadrado pode ser analisado como uma figura plana, fechada, de lados iguais e possuindo quatro lados. Apliquemos essa análise à verdade necessária “Um quadrado tem quatro lados” e obteremos: uma figura que é plana, fechada, eqüilateral e que possui quatro lados tem quatro lados, o que é uma identidade. Igualmente, na álgebra quando em uma equação (correta) substituímos valores, para suas variáveis, obtemos uma identidade. Por exemplo, na equação:
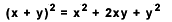
se substituirmos x por 2 e y por 3 obteremos:
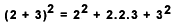
que resulta em: 25 = 4 + 12 + 5 donde 25 = 25 que é uma identidade. Assim, as verdades necessárias dependem do Princípio de Contradição, que estabelece que a negação de uma identidade nunca é verdadeira.
As verdades contingentes não podem ser reduzidas ao Princípio de Contradição. Se pudessem, não seriam contingentes e tudo seria necessário e nada seria possível exceto aquilo que existe atualmente.
Todavia, desde que afirmemos que tanto Deus como as criaturas existem e que as proposições necessárias e algumas contingentes são verdadeiras, deve haver uma noção de existência e uma noção de verdade que podem aplicar-se tanto àquilo que é contingente como ao que é necessário.
O que é comum a toda verdade, a meu ver, é que sempre se pode fornecer uma razão para uma proposição verdadeira a menos que seja uma identidade. Nas proposições necessárias a razão necessita [obriga], enquanto nas contingentes, inclina. Proposições idênticas são, como tenho afirmado, as razões fundamentais para todas as verdades necessárias; não temos razões do por que são verdadeiras.
E parece ser comum às coisas que existem, quer necessária quer contingentemente, que há mais razão para suas existências do que há para quaisquer outras existirem em seu lugar.
Toda proposição universal afirmativa verdadeira quer necessária quer contingente, possui alguma conexão entre sujeito e predicado. Em identidades esta conexão é auto-evidente; em outras proposições esta conexão tem de ser revelada através da análise dos termos.
Este fato pouco conhecido revela a distinção entre as verdades necessárias e as contingentes. Isto é difícil entender a menos que se disponha de algum conhecimento matemático. Quando a análise de uma proposição necessária é desenvolvida o suficiente, acaba por alcançar uma equação idêntica; isto é o que significa demonstrar uma verdade com rigor geométrico. Mas a análise de uma proposição contingente continua ao infinito, fornecendo-se razões (e razões para razões (e razões para aquelas razões…)), de modo que nunca se tem uma demonstração completa. Há sempre uma completa e final razão subjacente para a verdade da proposição, mas apenas Deus a compreende completamente, sendo Ele o único que pode se apossar da série infinita de um só golpe.
Posso ilustrar isso com um bom exemplo oriundo da geometria e dos números. Nas proposições necessárias, uma análise contínua do predicado e do sujeito pode eventualmente nos conduzir ao ponto onde podemos ver que a noção do predicado está na do sujeito. Para uma analogia numérica deste fato, considere-se o processo de obtenção de uma comparação exata entre dois números: repetidamente dividimos cada um deles até alcançarmos uma medida comum. Por exemplo: desejando comparar 24219 com 12558 percebemos que ambos podem ser divididos por 3, então, por 13, por 23, o que nos fornece uma relação mais inteligível: 27 por 14. Mas tal processo não funciona com um par de números irracionais tais como qualquer número inteiro e √2: como Euclides demonstrou, não há fração F (por mais diminuta que seja) tal que (F x F) = 2. Podemos examinar toda a série de frações, elevando cada termo ao quadrado, e nos aproximando de 2, mas nos é matematicamente impossível concluir a série encontrando uma fração cujo quadrado seja, exatamente, igual a 2. Ainda assim, há uma proporção ou relação entre, digamos, 3 e √2; não a podemos expressar exatamente em termos de frações, mas sabemos que existe: 3 é uma certa e determinada quantidade precisa maior que √2. Proponho esta analogia à situação das verdades contingentes: há nelas uma conexão entre os termos – isto é, há a verdade – mesmo que esta verdade não possa ser reduzida ao Princípio de Contradição ou necessidade através de uma análise em identidades.
Aqui estão duas questões que podem ser formuladas acerca da necessidade de certas proposições. A proposição “Deus escolhe o melhor” é necessária? Ou é um – na verdade, o primeiro – de Seus livres decretos? Outrossim, esta proposição “O que quer que exista, possui uma maior razão para existir do que para não existir” é necessária? Respondo que a primeira proposição não é necessária: Deus sempre escolhe o melhor porque Ele decreta que aquilo é o que Ele realizará. Disto decorre que a última proposição tampouco é necessária: há sempre uma razão maior para a existência de uma coisa atual do que para qualquer possível rival, mas apenas porque Deus livremente decidiu escolher sempre o melhor.
De certo há uma conexão entre sujeito e predicado em toda verdade. Portanto, a verdade de “Adão, que peca, existe” requer que a noção possível de “Adão que peca” envolva algo em virtude de que se afirma que ele existe.
Parece que devemos admitir que Deus sempre age sabiamente, isto é, de um modo tal que qualquer um que conhecesse Suas razões, conheceria e reverenciaria Sua justiça, bondade e sabedoria supremas. E parece que Deus nunca age de um modo determinado apenas porque Lhe agrada agir assim, a menos que haja uma boa razão pela qual isto Lhe agrada. [Assim, algo pode ser feito para a satisfação (vontade) divina, como diríamos, mas nunca como uma alternativa ao fato de ter sido feito por uma razão].
Desde que não podemos conhecer a verdadeira razão formal para a existência de qualquer coisa particular, porque isto envolveria uma série infinita de razões, temos que aceitar conhecer as verdades contingentes a posteriori, isto é, através da experiência. Mas devemos, ao mesmo tempo, sustentar o princípio geral, por Deus implantado em nossos espíritos e confirmado tanto pela razão como pela experiência, segundo o qual nada acontece sem uma razão, bem como o princípio dos contrários, segundo o qual, de possibilidades rivais, sempre acontece aquela para a qual há mais razão (eu afirmo “confirmado pela experiência”, mas trato isto cautelosamente. Quis dizer apenas que a experiência confirma o princípio na medida em que podemos descobrir razões por meio da experiência).
E assim como Deus decretou que Ele sempre agirá de acordo com verdadeiras razões de sabedoria, assim também Ele criou as criaturas racionais de um modo tal que atuem de acordo com as razões predominantes e “inclinantes” – razões que são verdadeiras ou, na sua ausência, lhes parecem ser verdadeiras.
A menos que existisse um tal princípio, aquele acerca das razões, não haveria princípio de verdade nas coisas contingentes, pois para estas, o Princípio de Contradição é certamente irrelevante.
Nem todos os possíveis alcançam a existência – temos que acentuar isto pois se isto fosse falso não poderíamos imaginar qualquer história que não fosse realmente verdadeira em algum lugar e tempo! De qualquer modo, não parece possível que todas as coisas possíveis existam, pois iriam tolher o passo umas das outras. De fato, há infinitamente muitas séries de coisas possíveis, nenhuma das quais pode estar contida dentro das demais, pois cada uma delas é completa.
Dos seguintes dois princípios, outros decorrem:
1. O que quer que Deus faça traz a marca da perfeição e sabedoria;
2. Nem todos os possíveis vêm à existência;
A estes, outro pode ser acrescentado:
3. Em toda proposição universal afirmativa verdadeira o predicado está no sujeito, isto é, há uma conexão entre o predicado e o sujeito.
Assumindo que esta proposição: “A proposição P que possui a maior razão para ser verdade é verdade” é necessária, devemos ver se, então, decorre que a própria P é necessária. Não é. Se, por definição, uma proposição necessária é aquela cuja verdade pode ser demonstrada com rigor geométrico, então, de fato poderia ocorrer que essas duas proposições são demonstráveis e, assim, necessárias.
Toda verdade e apenas uma verdade possui uma razão maior. Deus sempre age com a sabedoria suprema. Mas disto não se pode demonstrar qualquer proposição da forma: “A proposição contingente P possui maior razão para ser verdadeira que a proposição contingente não-P” ou da forma “A proposição contingente P está em conformidade com a sabedoria divina”. Então, das duas proposições acima não resulta que qualquer proposição contingente P é necessária. Assim, embora se possa admitir que “é necessário, para Deus, escolher o melhor”, ou que “o melhor é necessário”, não resulta que “P é necessário”, onde P é algo que foi escolhido; pois não há demonstração de que “P é o melhor”. Isto pode ser colocado em termos da distinção técnica entre necessidade da conseqüência e necessidade do conseqüente – ou seja, entre “P necessariamente resulta de Q” e “P é necessário por si mesmo”. Assumindo-se que o melhor é escolhido necessariamente, temos: a partir de “P é o melhor” resulta necessariamente que “P é verdadeiro”, mas não temos: “Necessariamente P é verdadeiro”, pois não demonstramos que “P é o melhor”.
Embora eu tenha examinado as implicações da tese segundo a qual necessariamente Deus sempre escolhe o melhor, eu não a sustento. Apenas afirmo que parece seguro atribuir a Deus o mais perfeito meio possível de direção. Quando se aplica às criaturas, não se pode estar certos (tal como estamos certos em relação a Deus) que agirão de acordo com, até mesmo, a mais óbvia razão; com relação às criaturas, esta proposição – que sempre agirão assim – não pode ser demonstrada.